Neutron Star Equation of State with Induced Surface Tension
Introduction
Compact stars are among the most exotic objects in the Universe, the matter in their interior being exposed to exceptionally high pressure, temperature and density. For that reason the cores of such stars’ are the unique laboratories to study and test the properties of strongly interacting matter in extreme conditions.
To understand the complex physical phenomena occurring inside such compact astrophysical objects an unique equation of state (EoS) that can simultaneously satisfy the experimental constraints obtained from nucleon-nucleon collision experiments, and the observational data coming from compact stars is required. To that end, we need to develop a profound understanding of the complex physical phenomena occurring to strongly interacting matter in extreme conditions. This requires a thorough knowledge of a wide range of scientific disciplines in physics, as well as a robust analysis of a large amount of observational and experimental data.
We developed the novel EoS, which includes the induced surface tension (IST) generated by the interparticle interaction, the so-called IST EoS [1], and the asymmetry between neutrons and protons, to the study of neutron star (NS) properties. This novel EoS is obtained from the virial expansion for the multicomponent particle mixtures that takes into account the hard-core repulsion between them.
As it is shown by Bugaev et. al. (2018) this theoretical framework gives us a precise description of the properties of nuclear matter [1], hadron multiplicities measured at the Alternating Gradient Synchrotron (AGS), the Super Proton Synchrotron (SPS), the Relativistic Heavy Ion Collider (RHIC), and the Large Hadron Collider (LHC) collision energies [2]. Moreover, this EoS satisfies the proton flow constraints [3], as well as the asymmetry energy constraint between neutrons and protons, and the data obtained from the observations of compact objects [4,5]. Fig. 1 shows the mass-radius relation for NS, for two different sets of parameters (A and B, see details in Table 1) of this new EoS. For more details see Ref. [5].
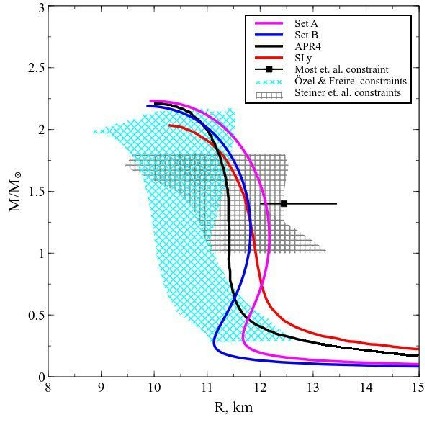
Figure 1: The mass-radius (or M-R) relation determines an unique correspondence between the gravitational total mass (M) and the total radius (R) of a NS. Therefore, such relation is the first observational test that any EoS must satisfy. The calculation of the IST EoS was performed for two different sets of parameters (A and B, see Table 1) which satisfy all the constraints mentioned above, and the found mass-radius relations lay inside the most likely regions of the parameter space, according to recent astrophysical observations [5]. These two new mass-radius relations are also compared with the well-known APR4 [6] and Sly [7] EoS.

Table 1: Sets of IST EoS parameters, which simultaneously reproduced the nuclear matter ground state properties, the flow constraints, and simultaneously predict a realistic critical endpoint of nuclear matter. The adjustable parameters of the model include r, α, κ, Bsym, Asym, Cd2 , and U0, whereas K0, J, L and Mmax are calculated for each of these sets (See Ref. [5] for details).
Here you can download the tabulated IST EoS for two sets of parameters (details in Table 1 and in Ref. [5])
References
- V.V. Sagun, A.I. Ivanytskyi, K.A. Bugaev, I.N. Mishustin, The statistical multifragmentation model for liquid-gas phase transition with a compressible nuclear liquid, Nucl. Phys. A, 924, 24 (2014);
- K.A. Bugaev, V.V. Sagun, A.I. Ivanytskyi, I.P. Yakimenko, E.G. Nikonov, A.V. Taranenko, G.M. Zinovjev, Going beyond the second virial coefficient in the hadron resonance gas model, Nucl. Phys. A, 970, 133 (2018);
- A. I. Ivanytskyi, K. A. Bugaev, V. V. Sagun, L.V. Bravina, E. E. Zabrodin, Influence of flow constraints on the properties of the critical endpoint of symmetric nuclear matter, Phys. Rev. C 97 064905 (2018);
- V.V. Sagun, I. Lopes, Neutron stars: A novel equation of state with induced surface tension, Astrophys. J, 850, 75 (2017);
- V. V. Sagun, I. Lopes, A. I. Ivanytskyi, The induced surface tension contribution for the equation of state of neutron stars, Preprint arXiv: 1805.04976v2 [astro-ph.HE] (2018);
- A. Akmal, V. R. Pandharipande, D. G. Ravenhall, Equation of state of nucleon matter and neutron star structure, Phys. Rev. C 58, 1804 (1998);
- F. Douchin, P. Haensel, A unified equation of state of dense matter and neutron star structure, Astron. & Astrophys. 380, 151 (2001).
Basic References
to be cited while using in a publication the results
- V.V. Sagun, I. Lopes, Neutron stars: A novel equation of state with induced surface tension, Astrophys. J, 850, 75 (2017);
- V. V. Sagun, I. Lopes, A. I. Ivanytskyi, The induced surface tension contribution for the equation of state of neutron stars, Preprint arXiv: 1805.04976v2 [astro-ph.HE] (2018);
- https://centra.tecnico.ulisboa.pt/network/costar/files/ist/ (this page)
