Referenciais e Rotação

Transformação das coordenadas de posição

O movimento dum ponto material depende do observador e do seu próprio estado de movimento. Em geral, dados dois sistemas de referência, $\mathrm{ℛ}$ = {$O,{\overrightarrow{e}}_x$,${\overrightarrow{e}}_y$,${\overrightarrow{e}}_z$} e ${\mathrm{ℛ}}^{ \prime }$ = {$O^{\prime }$,$\overrightarrow{e}{\mathrm{}}_x^{\prime }$,$\overrightarrow{e}{\mathrm{}}_y^{\prime }$,$\overrightarrow{e}{\mathrm{}}_z^{\prime }$}, que se deslocam e rodam um em relação ao outro (i.e. as direcções de referência não permanecem paralelas), a transformação de coordenadas cartesianas dum vector $\overrightarrow{r}$ do referencial $ℛ$ para o referencial ${ℛ}^{\prime }$, cuja origem é sempre dada por ${\overrightarrow{R}}_{O^{\prime } }$, é

$\overrightarrow{r}{\mathrm{}}^{\prime }=\mathbb{M}·\mathrm{(}\overrightarrow{r}{-\overrightarrow{R}}_{O^{\prime }}\mathrm{)}$

onde $\mathbb{M}$ é a transformação linear determinada, no sistema $\mathcal{S}$, pela matriz

$\mathbb{M}=\left|\hspace{0.17em}\begin{array}{ccc}\overrightarrow{e}{\mathrm{}}_x^{\prime }·{\overrightarrow{e}}_x& \overrightarrow{e}{\mathrm{}}_x^{\prime }·{\overrightarrow{e}}_y& \overrightarrow{e}{\mathrm{}}_x^{\prime }·{\overrightarrow{e}}_z\\ \overrightarrow{e}{\mathrm{}}_y^{\prime }·{\overrightarrow{e}}_x& \overrightarrow{e}{\mathrm{}}_y^{\prime }·{\overrightarrow{e}}_y& \overrightarrow{e}{\mathrm{}}_y^{\prime }·{\overrightarrow{e}}_z\\ \overrightarrow{e}{\mathrm{}}_z^{\prime }·{\overrightarrow{e}}_x& \overrightarrow{e}{\mathrm{}}_z^{\prime }·{\overrightarrow{e}}_y& \overrightarrow{e}{\mathrm{}}_z^{\prime }·{\overrightarrow{e}}_z\end{array}\hspace{0.17em}\right|$

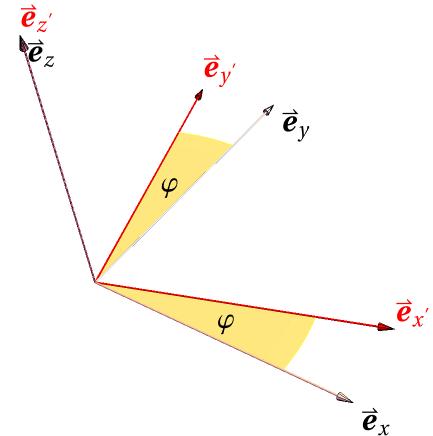
Por exemplo, para os sistemas $\mathrm{ℛ}$ e ${\mathrm{ℛ}}^{ \prime }$, com este último rodado em torno do eixo ${\overrightarrow{e}}_z\equiv \overrightarrow{e}{\mathrm{}}_z^{\prime }$ de $\mathrm{ℛ}$ por um ângulo $\phi$, como indicado na figura, obtemos

$\mathbb{M}=\left|\hspace{0.17em}\begin{array}{lll} \cos \left(\phi \right)& \cos \left(\frac{\pi }{2}-\phi \right)& 0\\ \cos \left(\frac{\pi }{2}+\phi \right)& \cos \left(\phi \right)& 0\\ 0& 0& 1\end{array}\hspace{0.17em}\right|=\left|\begin{array}{lll} \cos \left(\phi \right)& \sin \left(\mathrm{\phi }\right)& 0\\ -\sin \left(\phi \right)& \cos \left(\phi \right)& 0\\ \mathrm{ 0}& \mathrm{ 0}& 1\end{array}\hspace{0.17em}\right|$

Pela sua construção, $\mathbb{M}$ é uma matriz ortogonal, i.e. ${\mathbb{M}}^T\mathbb{M}\mathrm{ \equiv }\mathbb{M}{\mathbb{M}}^T\mathrm{= }\mathbb{1}$. Uma matriz destas possui valores próprios de módulo unidade (porque as rotações e reflexões preservam comprimentos), e um deles tem que ser real, $\lambda =\pm 1$ (porque a equação dos valores próprios é cúbica). O sinal depende de existirem, $(-)$, ou não, $(+)$, reflexões incluídas em $\mathbb{M}$. A direcção dum vector próprio $\overrightarrow{n}$ correspondente ao valor próprio real $\lambda =+1$ é invariante para a transformação ortogonal $\overrightarrow{n}{\mathrm{}}^{\prime }=\mathbb{M}·\overrightarrow{n}=\overrightarrow{n}$ e define assim o eixo de rotação da transformação.
Por outro lado, se os produtos $\overrightarrow{e}{\mathrm{}}_i^{\prime }·{\overrightarrow{e}}_j=cos\mathrm{(}{\theta }_{ij}\mathrm{)}$ variarem no tempo, $\mathbb{M}$ também é variável no tempo, mas $\frac{d}{dt}\mathrm{(}\mathbb{M}{\mathbb{M}}^T\mathrm{)}\equiv 0$ . Daqui se vê que, fazendo $\mathbb{W}=\frac{d\mathbb{M}}{dt}\mathrm{\hspace{0.17em}}{\mathbb{M}}^T$,

W + W T = ⅆ M ⅆ t M T + M ⅆ M T ⅆ t = 0

Propriedades Gerais

Uma matriz que verifique ${\mathbb{W}=-\mathbb{W}}^T$ diz-se anti-simétrica e tem a forma

$\mathbb{W}=\left|\hspace{0.17em}\begin{array}{rrr}0& -c& b\\ c& 0& -a\\ -b& a& 0\end{array}\hspace{0.17em}\right|$

Em três dimensões existe sempre um vector $\overrightarrow{\omega }=\mathrm{\{}{\omega }_1,{\omega }_2,{\omega }_3\mathrm{\}}=-\mathrm{\{}a,b,c\mathrm{\}}$ associado matriz anti-simétrica $\mathbb{W}$, tal que, para qualquer vector $\overrightarrow{b}$:

$\mathbb{W}·\overrightarrow{b}=-\overrightarrow{\omega }\mathrm{\times }\overrightarrow{b}$

Por simetria se vê que, fazendo ${\mathbb{W}}^{\prime }\equiv \mathbb{M}\mathrm{\hspace{0.17em}}\mathbb{W}\mathrm{\hspace{0.17em}}{\mathbb{M}}^T$ , também ${\mathbb{W}}^{\prime }=\; -{{\mathbb{W}}^{\prime }}^T$ e portanto

$\mathbb{W}{\mathrm{}}^{\prime }·\overrightarrow{b}{\mathrm{}}^{\prime }=\mathbb{M}\mathrm{\hspace{0.17em}}{\mathbb{W}}^{}\mathrm{\hspace{0.17em}}{\mathbb{M}}^T·\overrightarrow{b}{\mathrm{}}^{\prime }=-\mathbb{M}·\mathrm{(}\overrightarrow{\omega }\mathrm{\times }\mathrm{(}{\mathbb{M}}^T·\overrightarrow{b}{\mathrm{}}^{\prime }\mathrm{)}\mathrm{)}=-\mathrm{(}\mathbb{M}·\overrightarrow{\omega }\mathrm{)}\mathrm{\times }\overrightarrow{b}{\mathrm{}}^{\prime }=-\overrightarrow{\omega }{\mathrm{}}^{\prime }\mathrm{\times }\overrightarrow{b}{\mathrm{}}^{\prime }$

porque a matriz ortogonal $\mathbb{M}$ verifica $\mathbb{M}·\mathrm{(}\overrightarrow{a}\mathrm{\times }\overrightarrow{c}\mathrm{)}=\mathrm{(}\mathbb{M}·\overrightarrow{a}\mathrm{)}\mathrm{\times }\mathrm{(}\mathbb{M}·\overrightarrow{c}\mathrm{)}$.

Transformação da Velocidade

No caso da matriz anti-simétrica $\mathbb{W}=\frac{d\mathbb{M}}{dt}{\mathbb{M}}^T$, a associação com o vector $\overrightarrow{\omega }$ traduz–se na identificação $\overrightarrow{\omega }\equiv \overrightarrow{\omega }{}^{\prime }=\mathbb{M}·\overrightarrow{\omega }$ (porque $\mathbb{M}·\omega \overrightarrow{n}=\omega \overrightarrow{n}{}^{\prime }=\omega \overrightarrow{n}$), onde $\overrightarrow{\omega }$ é a velocidade angular (de rotação das direcções de referência) de ${\mathcal{S}}^{\prime }$ em $\mathcal{S}$.

Note que, como $\mathbb{M}$ é ortogonal, ${\mathbb{M}}^T$≡${\mathbb{M}}^{-1}$ e assim $\mathrm{(}\overrightarrow{r}-{\overrightarrow{R}}_{O^{\prime }}\mathrm{)}={\mathbb{M}}^T·\overrightarrow{r}{}^{\prime }$ e portanto

v → ′ = ⅆ r → ′ ⅆ t = M · ( v → − V → O ′ ) + ⅆ M ⅆ t · ( r → − R → O ′ ) = M · ( v → − V → O ′ ) + ⅆ M ⅆ t ⁢ M T · r → ′ ≡ M · ( v → − V → O ′ ) + W · r → ′

ou seja

v → ′ = M · ( v → − V → O ′ ) − ω → ′ × r → ′

Transformação da Aceleração

Pode-se agora calcular o que será a aceleração ${\overrightarrow{a}}^{}{\mathrm{}}^{\prime }=\frac{d{\overrightarrow{v}}^{}}{dt}$ :

a → ′ = M · ( a → − A → O ′ ) + ⅆ M ⅆ t · ( v → − V → O ′ ) − ω → ′ × v → ′ − ⅆ ω → ′ ⅆ t × r → ′

Substituindo nesta expressão $\mathrm{(}\overrightarrow{v}-{\overrightarrow{V}}_{O^{\prime }}\mathrm{)}={\mathbb{M}}^T·\mathrm{(}\overrightarrow{v}{}^{\prime }+\overrightarrow{\omega }{}^{\prime }\mathrm{\times }\overrightarrow{r}{}^{\prime }\mathrm{)}$ e relembrandro que $\mathbb{W}=\frac{d\mathbb{M}}{dt} {\mathbb{M}}^T$ e que $\overrightarrow{\omega }\equiv \overrightarrow{\omega }{}^{\prime }$ ,

a → ′ = M · ( a → − A → O ′ ) − ω → ′ × ( v → ′ + ω → ′ × r → ′ ) − ω → ′ × v → ′ − ⅆ ω → ′ ⅆ t × r → ′

a → ′ = M · ( a → − A → O ′ ) − ω → ′ × ( ω → ′ × r → ′ ) − 2 ⁢ ω → ′ × v → ′ − ⅆ ω → ′ ⅆ t × r → ′

NB: $\frac{d\overrightarrow{\omega }{}^{\prime }}{dt}=\frac{d}{dt}\mathrm{(}\mathbb{M}·\overrightarrow{\omega }\mathrm{)}=\frac{d\mathbb{M}}{dt}·\overrightarrow{\omega }+\mathbb{M}·\frac{d\overrightarrow{\omega }}{dt}=-\overrightarrow{\omega }\mathrm{\times }\overrightarrow{\omega }{}^{\prime }+\mathbb{M}·\frac{d\overrightarrow{\omega }}{dt}\equiv \mathbb{M}·\frac{d\overrightarrow{\omega }}{dt}$.

Além disso, uma matriz ortogonal $\mathbb{M}$ verifica $\mathbb{M}·\mathrm{(}\overrightarrow{a}\mathrm{\times }\overrightarrow{b}\mathrm{)}=\mathrm{(}\mathbb{M}·\overrightarrow{a}\mathrm{)}\mathrm{\times }\mathrm{(}\mathbb{M}·\overrightarrow{b}\mathrm{)}$ (as transformações ortogonais preservam os ângulos entre vectores e as normas destes). Assim a expressão para $\overrightarrow{a}{}^{\prime }$ pode ainda escrever–se, designando por $\overrightarrow{\alpha }=\frac{d\overrightarrow{\omega }}{dt}$ a aceleração angular de ${ℛ}^{\hspace{0.17em}\prime }$em $ℛ$, e fazendo $\frac{d\overrightarrow{\omega }{}^{\prime }}{dt}=\mathbb{M}·\frac{d\overrightarrow{\omega }}{dt}=\mathbb{M}·\overrightarrow{\alpha }$:

$\begin{array}{cccccc}\overrightarrow{a}{}^{\prime }=& \mathbb{M}·\mathrm{(}\overrightarrow{a}-{\overrightarrow{A}}_{O^{\prime }}\mathrm{)}& - \overrightarrow{\omega }{}^{\prime }\mathrm{\times }\mathrm{(}\overrightarrow{\omega }{}^{\prime }\mathrm{\times }\overrightarrow{r}{}^{\prime }\mathrm{)}& - \mathrm{2 }\overrightarrow{\omega }{}^{\prime }\mathrm{\times }\overrightarrow{v}{}^{\prime }& - \mathbb{M}·\mathrm{(}\overrightarrow{\alpha }\mathrm{\times }\mathrm{(}\overrightarrow{r}-{\overrightarrow{R}}_{O^{\prime }}\mathrm{)}\mathrm{)}& \\ & \underset{\mathrm{Relativa}}{\overset{}{⏟}}& \underset{\mathrm{Centrífuga}}{\overset{}{⏟}}& \underset{\mathrm{Coriolis}}{\overset{}{⏟}}& \underset{\mathrm{Euler}}{\overset{}{⏟}}& \end{array}$

© Amaro Rica da Silva, Prof. Dep. Física-IST with Mathematica  (September 20, 2005)