Collisions.xml

Colisão Elástica de duas partículas de massas $m_{1}, m_{2}$

Java Applet: Colisões elásticas de duas partículas.

Use Shift-Drag para Zoom; Use Left-Drag para rodar; Pontos (e vectores) selectionáveis apresentam um pequeno quadrado quando apontados pelo cursor, e podem então ser movidos com Left-Drag.

Colisão e trajetórias com interação atractiva.

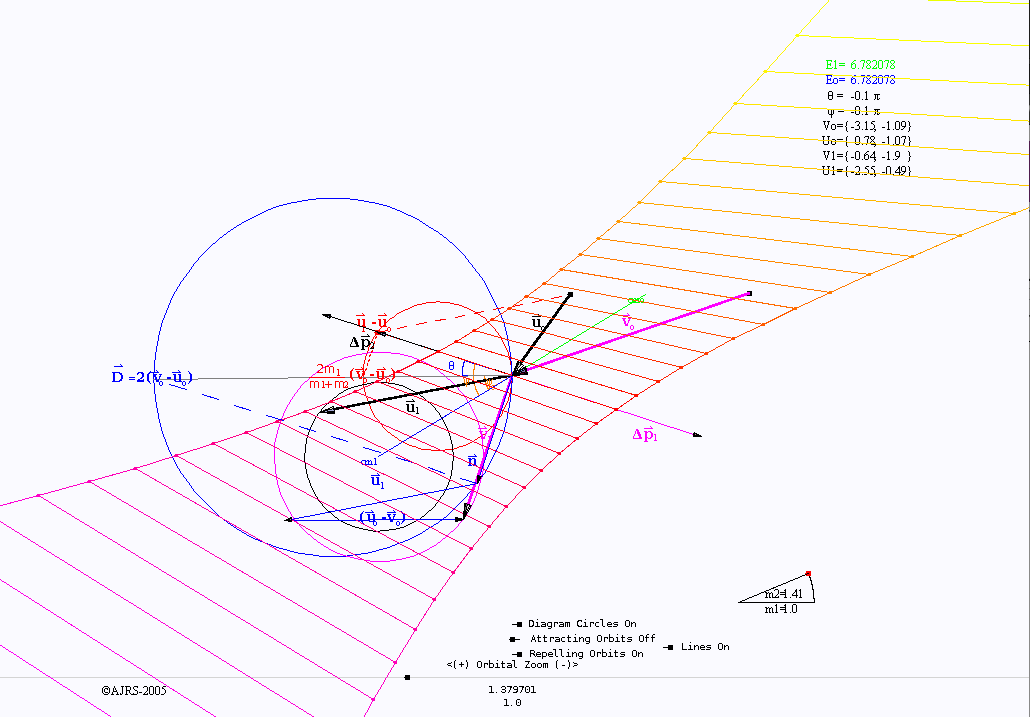
Colisão e trajetórias com interação repulsiva.

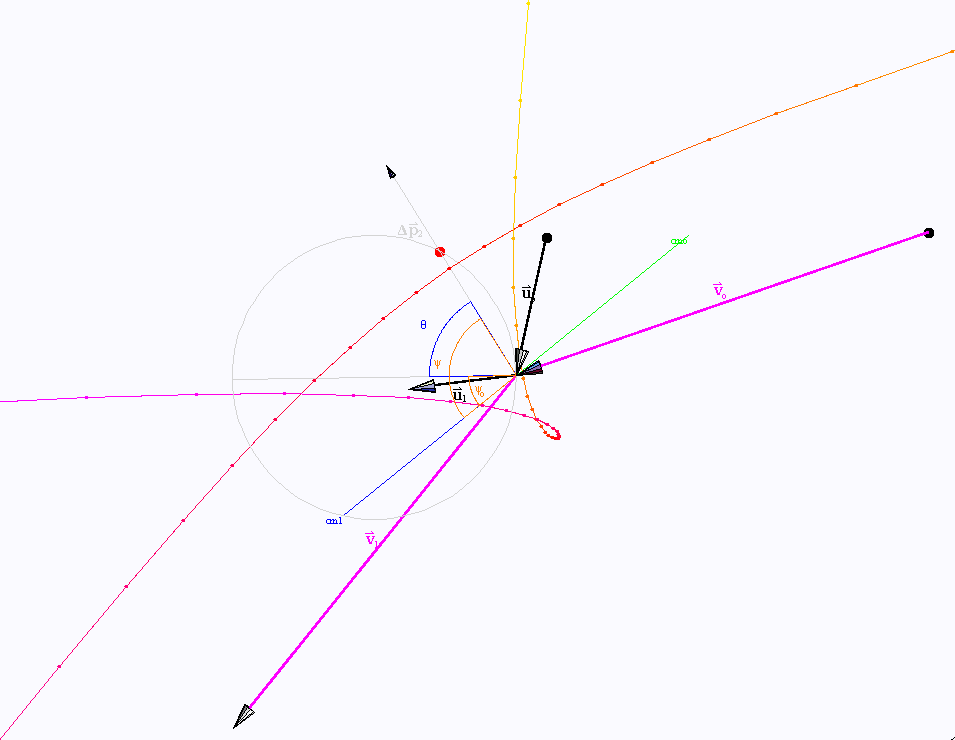
Colisão e trajetórias com interação atractiva.

Uma partícula em repouso (ou referencial próprio duma partícula)

Leis de Conservação

{\begin{cases} \begin{matrix} m_{1} {\vec{v}}_{o} = m_{1} {\vec{v}}_{1} + m_{2} {\vec{u}}_{1} \\ \frac{1}{2} m_{1} v_{o}^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} u_{1}^{2} \end{matrix} \end{cases} \Leftrightarrow {\begin{cases} \frac{m_{1}}{m_{2}} ({\vec{v}}_{o} − {\vec{v}}_{1}) = {\vec{u}}_{1} \\ \frac{m_{1}}{m_{2}} ({\vec{v}}_{o} − {\vec{v}}_{1}) \cdot ({\vec{v}}_{o} + {\vec{v}}_{1}) = {\vec{u}}_{1} \cdot {\vec{u}}_{1} \end{cases}

(1)

Determinação de ${\vec{u}}_{1}$

Substituindo $\frac{m_{1}}{m_{2}}$ ( ${\vec{v}}_{o} − {\vec{v}}_{1}$ ) por ${\vec{u}}_{1}$ no lado esquerdo, e ${\vec{u}}_{1}$ por $\frac{m_{1}}{m_{2}}$ ( ${\vec{v}}_{o} − {\vec{v}}_{1}$ ) no lado direito, da última equação de (1) obtemos

${\vec{u}}_{1} \cdot ({\vec{v}}_{o} + {\vec{v}}_{1}) = {\vec{u}}_{1} \cdot (\frac{m_{1}}{m_{2}} ({\vec{v}}_{o} − {\vec{v}}_{1})) \Rightarrow {\vec{u}}_{1} \cdot ((1 − \frac{m_{1}}{m_{2}}) {\vec{v}}_{o} + (1 + \frac{m_{1}}{m_{2}}) {\vec{v}}_{1}) = 0$

donde

{\vec{v}}_{1} \cdot {\vec{u}}_{1} = \frac{m_{1} − m_{2}}{m_{1} + m_{2}} {\vec{v}}_{o} \cdot {\vec{u}}_{1}

(2)

Multiplicando a primeira equação em (1) por ${\vec{u}}_{1}$ e substituindo aí este resultado (2) obtém-se

{\vec{u}}_{1} \cdot {\vec{u}}_{1} = \frac{m_{1}}{m_{2}} ({\vec{v}}_{o} \cdot {\vec{u}}_{1} − {\vec{v}}_{1} \cdot {\vec{u}}_{1}) = \frac{m_{1}}{m_{2}} ({\vec{v}}_{o} \cdot {\vec{u}}_{1} − \frac{m_{1} − m_{2}}{m_{1} + m_{2}} {\vec{v}}_{o} \cdot {\vec{u}}_{1}) = \frac{2 m_{1}}{m_{1} + m_{2}} {\vec{v}}_{o} \cdot {\vec{u}}_{1}

(3)

Designando a direcção de ${\vec{u}}_{1}$ por ${\vec{u}}_{θ}$ = $\frac{{\vec{u}}_{1}}{\sqrt{{\vec{u}}_{1} \cdot {\vec{u}}_{1}}}$ , esta expressão (3) dá-nos a sua magnitude $u_{1}$ = $\sqrt{{\vec{u}}_{1} \cdot {\vec{u}}_{1}}$

$u_{1} = \frac{2 m_{1}}{m_{1} + m_{2}} {\vec{v}}_{o} \cdot {\vec{u}}_{θ}$

Conhecido $θ$ , isto determina completamente ${\vec{u}}_{1}$

{\vec{u}}_{1} = \frac{2 m_{1}}{m_{1} + m_{2}} v_{o} \cos (θ) {\vec{u}}_{θ}

(4)

Escrito doutra maneira, designando $\vec{d}$ = $\frac{2 m_{1}}{m_{1} + m_{2}}$ ${\vec{v}}_{o} = 2 {\vec{V}}_{cm}$ em (3),

${\vec{u}}_{1} \cdot {\vec{u}}_{1} = \vec{d} \cdot {\vec{u}}_{1} \Rightarrow (\vec{d} − {\vec{u}}_{1}) \cdot {\vec{u}}_{1} = 0$

Conclui-se assim que $\vec{d} − {\vec{u}}_{1}$ é perpendicular a ${\vec{u}}_{1}$ , isto é, ${\vec{u}}_{1}$ é uma corda num círculo de diâmetro $d = \frac{2 m_{1}}{m_{1} + m_{2}}$ $v_{o}$ e centro em $\frac{1}{2}$ $\vec{d} = {\overset{⇀}{V}}_{cm}$ (vide Fig 1). Logo, designando por $θ ∈ [- \frac{π}{2}$ , $\frac{π}{2}$ ] o ângulo entre ${\vec{v}}_{o}$ e ${\vec{u}}_{1}$ , deduziríamos directamente da geometria que

$(\vec{d} − {\vec{u}}_{1}) ⊥ {\vec{u}}_{1} \Rightarrow u_{1} = d \cos (θ) = \frac{2 m_{1}}{m_{1} + m_{2}} v_{o} \cos (θ)$

[Graphics:HTMLFiles/AmaroFig2.png]

Figura 1

Construção geométrica

Contudo, para uma determinação puramente geométrica de ${\vec{v}}_{1}$ , agora que conhecemos ${\vec{u}}_{1}$ , devemos escrever a segunda equação de (1), substituindo $\frac{m_{1}}{m_{2}}$ ( ${\vec{v}}_{o} − {\vec{v}}_{1}$ ) por ${\vec{u}}_{1}$ no lado esquerdo, na forma

${\vec{u}}_{1} \cdot ({\vec{v}}_{o} + {\vec{v}}_{1} − {\vec{u}}_{1}) = 0$

Podemos concluir que ${\vec{v}}_{o}$ + ${\vec{v}}_{1} − {\vec{u}}_{1}$ = $\vec{n}$ , não sendo nulo, é um vector perpendicular a ${\vec{u}}_{1}$ porque verifica ${\vec{u}}_{1}$ · $\vec{n}$ =0. Daqui se deduz a expressão para ${\vec{v}}_{1}$

{\vec{v}}_{o} + {\vec{v}}_{1} − {\vec{u}}_{1} = \vec{n} \Rightarrow {\vec{v}}_{1} = {\vec{u}}_{1} − {\vec{v}}_{o} + \vec{n}

(5)

Multiplicando a primeira equação em (1) por este $\vec{n}$ obtemos, substituindo (5),

\frac{m_{1}}{m_{2}} \vec{n} \cdot ({\vec{v}}_{o} − {\vec{v}}_{1}) = 0 \Rightarrow \vec{n} \cdot (2 {\vec{v}}_{o} − \vec{n}) = 0

\vec{n} = 2 v_{o} \cos (\frac{π}{2} − θ) {\vec{w}}_{θ} = 2 v_{o} \sin (θ) {\vec{w}}_{θ}

(6)

onde a última expressão decorre do facto de 2 ${\vec{v}}_{o} − \vec{n}$ ser perpendicular a $\vec{n}$ , o que significa que $\sqrt{\vec{n} \cdot \vec{n}}$ =2 ${\vec{v}}_{o}$ · ${\vec{w}}_{θ}$ onde ${\vec{w}}_{θ}$ = $\frac{\vec{n}}{\sqrt{\vec{n} \cdot \vec{n}}}$ é o vector unitário na direcção de $\vec{n}$ , e portanto perpendicular a ${\vec{u}}_{1}$ e ${\vec{u}}_{θ}$ tal como anteriormente referido. Como impusemos ${\vec{v}}_{o}$ · ${\vec{u}}_{θ}$ = $v_{o}$ Cos[θ], sabemos que o que deve corresponder a ${\vec{v}}_{o}$ · ${\vec{w}}_{θ}$ = $v_{o}$ Sin[θ], donde resulta (6). Substituindo (4) , (8) e (6) em (5) obtemos

{\vec{v}}_{1} = {\vec{u}}_{1} − {\vec{v}}_{o} + \vec{n} = \cos (θ) (\frac{m_{1} − m_{2}}{m_{1} + m_{2}}) v_{o} {\vec{u}}_{θ} + \sin (θ) v_{o} {\vec{w}}_{θ}

(7)

Determinação de ${\vec{v}}_{1}$ a partir da Lei de Conservação do Momento Linear

Da conservação do momento linear em (1) devemos obter ${\vec{v}}_{1}$ : se usarmos (4) e escrevermos

{\vec{v}}_{o} = v_{o} \cos (θ) {\vec{u}}_{θ} + v_{o} \sin (θ) {\vec{w}}_{θ}

(8)

onde ${\vec{w}}_{θ}$ representa o vector unitário perpendicular a ${\vec{u}}_{1}$ e paralelo a $\vec{d} − {\vec{u}}_{1}$ , obtemos de acordo com (7)

{\vec{v}}_{1} = {\vec{v}}_{o} − \frac{m_{2}}{m_{1}} {\vec{u}}_{1} = \cos (θ) (\frac{m_{1} − m_{2}}{m_{1} + m_{2}}) v_{o} {\vec{u}}_{θ} + \sin (θ) v_{o} {\vec{w}}_{θ}

(9)

O ângulo φ entre ${\vec{v}}_{1}$ e ${\vec{v}}_{o}$ determina-se agora como

\begin{array}{l} \cos (ϕ) = \frac{{\vec{v}}_{1} \cdot {\vec{v}}_{o}}{v_{1} v_{o}} = ((\frac{m_{1} − m_{2}}{m_{1} + m_{2}}) {\cos (θ)}^{2} + {\sin (θ)}^{2}) \frac{v_{o}}{v_{1}} = \frac{(\frac{m_{1} − m_{2}}{m_{1} + m_{2}}) {\cos (θ)}^{2} + {\sin (θ)}^{2}}{\sqrt{{(\frac{m_{1} − m_{2}}{m_{1} + m_{2}})}^{2} {\cos (θ)}^{2} + {\sin (θ)}^{2}}} \\ \cos (ϕ) = \frac{1 − \frac{2 m_{2}}{m_{1} + m_{2}} {\cos (θ)}^{2}}{\sqrt{1 − \frac{4 m_{1} m_{2}}{{(m_{1} + m_{2})}^{2}} {\cos (θ)}^{2}}} \end{array}

(10)

Apenas quando $m_{1}$ = $m_{2}$ (vide Fig. 2) se tem $cos (φ) = sin (θ)$ ou seja φ+θ= $\frac{π}{2}$ .

[Graphics:HTMLFiles/AmaroFig3.png]

Figura 2

Caso Geral

\begin{array}{l} {\begin{matrix} m_{1} {\vec{v}}_{o} + m_{2} {\vec{u}}_{o} = m_{1} {\vec{v}}_{1} + m_{2} {\vec{u}}_{1} \\ \frac{1}{2} m_{1} v_{o}^{2} + \frac{1}{2} m_{2} u_{o}^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} u_{1}^{2} \end{matrix} \Leftrightarrow {\begin{cases} \frac{m_{1}}{m_{2}} ({\vec{v}}_{o} − {\vec{v}}_{1}) = {\vec{u}}_{1} − {\vec{u}}_{o} \\ \frac{m_{1}}{m_{2}} ({\vec{v}}_{o} − {\vec{v}}_{1}) \cdot ({\vec{v}}_{o} + {\vec{v}}_{1}) = ({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} + {\vec{u}}_{o}) \end{cases} \end{array}

(11)

O mesmo tipo de raciocínio que anteriormente leva-nos a concluir de (11)

({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot {\vec{v}}_{1} = ({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot (\frac{2 m_{2}}{m_{1} + m_{2}} {\vec{u}}_{o} + \frac{(m_{1} − m_{2})}{m_{1} + m_{2}} {\vec{v}}_{o})

(12)

Multiplicando a primeira equação em (11) por ${\vec{u}}_{1} − {\vec{u}}_{o}$ e substituindo aí este resultado (12) obtém-se

({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} − {\vec{u}}_{o}) = \frac{2 m_{1}}{m_{1} + m_{2}} ({\vec{v}}_{o} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} − {\vec{u}}_{o})

(13)

Daí que se possa deduzir

\sqrt{({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} − {\vec{u}}_{o})} = \vec{d} \cdot {\vec{u}}_{θ}

(14)

onde

\vec{d} = \frac{2 m_{1}}{m_{1} + m_{2}} ({\vec{v}}_{o} − {\vec{u}}_{o}) = 2 ({\overset{⇀}{V}}_{cm} - {\overset{⇀}{u}}_{o}); {\vec{u}}_{θ} = \frac{({\vec{u}}_{1} − {\vec{u}}_{o})}{\sqrt{({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} − {\vec{u}}_{o})}}

(15)

${\vec{u}}_{θ}$ é a direcção de ${\vec{u}}_{1} − {\vec{u}}_{o}$ . Reescrevendo a equação (12) na forma

({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} − {\vec{u}}_{o}) = \vec{d} \cdot ({\vec{u}}_{1} − {\vec{u}}_{o}) \Rightarrow ({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} − {\vec{u}}_{o} − \vec{d}) = 0

(16)

concluimos como anteriormente que ${\vec{u}}_{1} − {\vec{u}}_{o}$ se localiza num círculo de diâmetro $\vec{d}$ . Finalmente, da segunda equação (11) obtém-se, por substituição da primeira no lado esquerdo

\frac{m_{1}}{m_{2}} ({\vec{v}}_{o} − {\vec{v}}_{1}) \cdot ({\vec{v}}_{o} + {\vec{v}}_{1}) = ({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot ({\vec{u}}_{1} + {\vec{u}}_{o}) \Leftrightarrow ({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot (({\vec{v}}_{o} + {\vec{v}}_{1}) − ({\vec{u}}_{1} + {\vec{u}}_{o})) = 0

(17)

o que indica

({\vec{v}}_{o} + {\vec{v}}_{1}) − ({\vec{u}}_{1} + {\vec{u}}_{o}) = \vec{n} && ({\vec{u}}_{1} − {\vec{u}}_{o}) \cdot \vec{n} = 0 ∴ {\vec{v}}_{1} = \vec{n} + {\vec{u}}_{1} − ({\vec{v}}_{o} − {\vec{u}}_{o})

(18)

Multiplicando a primeira equação em (11) por $\vec{n}$ obtém-se

\frac{m_{1}}{m_{2}} \vec{n} \cdot ({\vec{v}}_{o} − {\vec{v}}_{1}) = \vec{n} \cdot ({\vec{u}}_{1} − {\vec{u}}_{o}) = 0 ∴ \vec{n} \cdot ({\vec{v}}_{o} − \vec{n} − {\vec{u}}_{1} + ({\vec{v}}_{o} − {\vec{u}}_{o})) = \vec{n} \cdot (2 ({\vec{v}}_{o} − {\vec{u}}_{o}) − \vec{n}) = 0

(19)

Obtemos assim que $\vec{n}$ também se localiza num círculo de raio $\vec{D} = 2 ({\vec{v}}_{o} − {\vec{u}}_{o})$ sendo perpendicular a ${\vec{u}}_{1} − {\vec{u}}_{o} .$

[Graphics:HTMLFiles/AmaroFig5.png]

Figura 3

As velocidades finais ${\vec{u}}_{1}$ e ${\vec{v}}_{1}$ anteriormente definidas determinam dois circulos concêntricos, com centro em O+ ${\vec{V}}_{cm}$ = O+ $\frac{m_{1} {\vec{v}}_{1} + m_{2} {\vec{u}}_{1}}{m_{1} + m_{2}}$ após a colisão. Os respectivos raios serão

r_{u} = || {\vec{u}}_{1} − {\vec{V}}_{cm} ||; r_{v} = || {\vec{v}}_{1} − {\vec{V}}_{cm} || = || \frac{m_{2}}{m_{1}} ({\vec{V}}_{cm} − {\vec{u}}_{1}) ||

(20)

Como seria de esperar, as extremidades dos vectores ${\vec{u}}_{1}$ , ${\vec{v}}_{1}$ e ${\vec{V}}_{cm}$ estarão sempre numa linha recta depois da colisão. O diâmetro dos círculos anteriores coincide com a direcção de ${\vec{V}}_{cm}$ , e o máximo que pode atingir é 2|| ${\vec{u}}_{o} − {\vec{v}}_{o}$ ||, o que acontece quando uma das massas é muito superior à outra. Se por exemplo $m_{1}$ ≫ $m_{2}$ , então ${\vec{V}}_{cm}$ = ${\vec{v}}_{o}$ = ${\vec{v}}_{1}$ . Quando $\vec{n}$ =0 em geral ${\vec{v}}_{1} − {\vec{u}}_{1}$ = ${\vec{u}}_{o} − {\vec{v}}_{o}$ . Isto significa que quando $r_{v}$ →0, a diferença

{\vec{v}}_{1} − {\vec{u}}_{1}

||=||

{\vec{u}}_{o} − {\vec{v}}_{o}

|| →

r_{u}

=||

{\vec{V}}_{cm} − {\vec{u}}_{1}

(21)

Exemplos

[Graphics:HTMLFiles/AmaroFig1.png]

Figura 4 - $m_{2}$ Slingshot

[Graphics:HTMLFiles/AmaroFig9.png]

Figura 5 - $m_{2}$ Breaking